一種估算比特幣泡沫大小的科學方法

來源：劉教鏈

教鏈按：這是冪律理論的研究者之一Giovanni Santostasi的最新文章。

下面這篇文章，則是Giovanni Santostasi針對比特幣每4年一次的產量減半周期，在冪律增長模型的基礎上，對周期性泡沫的微觀建模。

我們在之前的文章中已經論證過，比特幣的長期表現是時間冪律。

鑑於冪律具有標度不變的特性，這使得我們在預測下一個數量級或兩個數量級的變化時有很大的把握，因爲比特幣已經有近 9 個數量級的標度不變性（如果我們把一些已知的最早的美元兌比特幣交易包括在內，在這些交易中，1 美元兌換 10,000 個比特幣）。

比特幣可預測的另一個重要特性是周期性。一個具有強大的已知周期性的系統也是可以預測的。

比特幣在 4 年的時間裏表現出精確的周期性，即比特幣周期。這些周期性與產量減半有關。

半衰期之後通常會有一個長約 1 年半的比平常更牛的時期。

在減半後的大約 1 年半時間裏，會觀察到與一般冪律趨勢的巨大偏差，這與局部最大值或周期的峰值相對應。然後，價格又快速下跌一年左右，達到周期的最低點或最低水平。價格再次緩慢上升，直到下一次減半，然後循環往復。

在比特幣 15 年的歷史中，這種特殊的序列發生過 3 次，模式非常相似。

有一個減半前的泡沫與任何減半都無關。它發生在比特幣誕生後的 4 年中，比第一次減半還要早。與其他泡沫相比，這個泡沫的行爲不規則（時間、泡沫高度和其他細節），因此我們將其排除在分析之外。

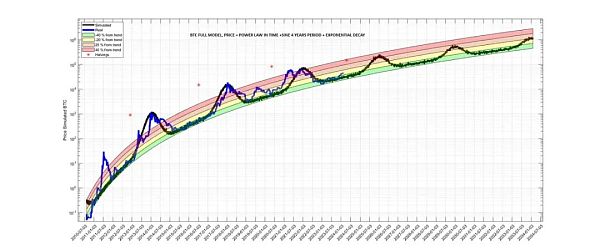
圖釋：比特幣的冪律行爲與趨勢存在偏差。圖中還展示了完整模型。可以看到 4 年周期的明顯振蕩。

通過觀察比特幣的價格走勢不難發現，峰值的高度似乎會隨着時間的推移而降低。估算這一高度的一個自然方法是觀察從趨勢的常規底部开始的變化。

我們自然會問，這種峰值高度的降低是否有特定的模式。

這個問題在過去已經討論過很多次，但最近引起我注意的一個特別的嘗試是彼得·勃蘭特（Peter Brandt）在 X 上所做的。

教鏈注：Peter Brandt的觀點是，根據每一輪周期從底到頂漲幅衰退推測，本輪周期的頂部就是72k —— 也就是說，這一輪牛市已經過頂了。而他認爲後續市場或回調至2021年的中期低點30k。

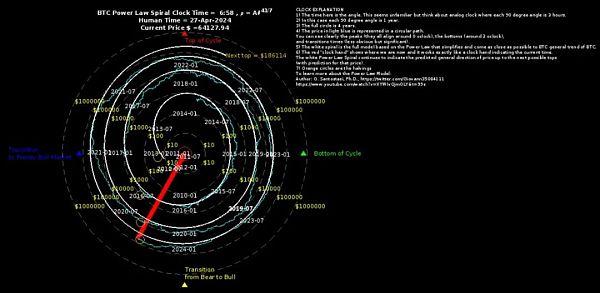
如果你想用時鐘時間來代替，12點 是頂部，3點 是底部，6點 是熊市向牛市的過渡，9點 是向全面牛市的過渡。

我們剛剛過了 6點，還沒有進入全面牛市，離周期中通常出現頂部的時間還很遠。

彼得·勃蘭特的結論來自以下觀察。

如果我們測量每個周期從底部到頂部的變化（他將減半前的時期包括在內，由於上述原因，我們將把這一時期排除在外），那么我們可以得出下表：（教鏈注：這是勃蘭特的表格）

如果用從底部算起的百分比變化來表示，似乎每個周期的高度都會降低 5 倍。如果不考慮減半前的時期，我們只有 3 個數據點；如果考慮比率，實際上只有 2 個數據點。這些數據不足以進行任何重要的統計分析。但是，如果我們想對下一個可能出現的比特幣泡沫規模做一些有根據的估計，考慮到我們只有這些數據，這也是一種可以接受的方法。

因此，如果我們從表面上看上表，就會得出這樣的結論：本輪比特幣泡沫將比歷史周期的底部 16500 美元只高出 4.5 倍，也就是說，頂部應該在 70000 美元左右。鑑於我們已經達到了這一數值，結論將是我們已經達到了頂峰，因此從現在开始只是下跌而已。

除了已經觀察到的周期時間問題，我們還有另一個問題。這種分析沒有考慮到比特幣的長期冪律軌跡。

從底部到頂部之間大約有 3 年的時間。在這些年裏，比特幣會沿着冪律軌跡大幅波動，然後通常會有 1 年的完整牛市。

我們可以使用 Desmos計算器應用程序來理解這一點。

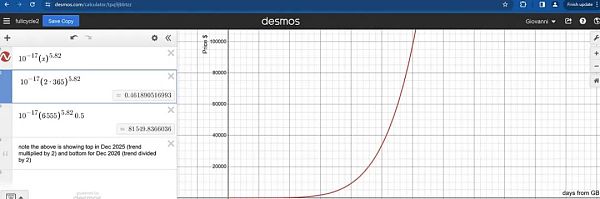
應用中已輸入的公式會告訴我們創世區塊（Genesis Block, GB）後某一天的冪律估計價格。第一個周期的底部應該發生在創世區塊之後的 3 年左右，因此趨勢值約爲 0.46 美元。

比特幣的實際價值約爲 0.3 美元。

底部 3 年後，我們迎來了第一個真正的泡沫，價值爲 1242 美元。頂部和底部之間的比率應該接近 4000 倍，而不是報告中的 572 倍。這打破了所宣稱的峰值從底部到頂部減少 5 倍的規律。

這是由於測量與比特幣周期中的周期性事件相關的底部和頂部，而沒有將減半前的泡沫作爲一個真正的泡沫。

這就證明了這種選取周期底部和頂部來估計峰值大小的方法的隨意性。

此外，峰值出現時的趨勢值接近 100 美元。

考慮到一般冪律趨勢，用偏離一般冪律趨勢的程度來衡量頂部似乎更爲自然。這可以通過計算價格相對於冪律趨勢的百分比差來實現。

下圖顯示了百分比差與時間的函數關系。

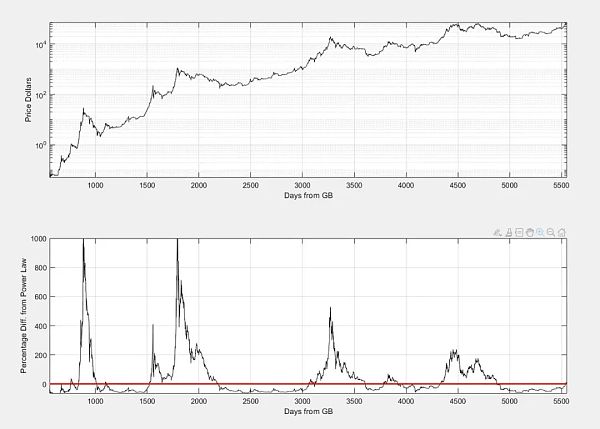
我們可以觀察到底部是非常有規律的，而且似乎發生在總體趨勢的-60%左右。

頂部似乎顯示了我們在常規比特幣價格走勢圖表中觀察到的典型衰減。

讓我們測量一下這些偏差，看看是否能觀察到某種模式。

讓我們看看能否繪制出這些數據點並找出其中的規律，而不是計算比率。快速衰減表明存在指數趨勢，在半對數圖中應顯示爲一條直线。我們用峰值數來擬合數據，而不是時間函數。

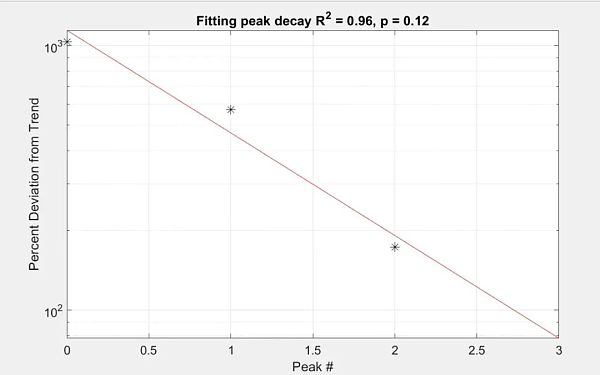
事實上，我們看到的擬合效果不錯，R² 值爲 0.96。皮爾遜系數至少要達到 0.05 才能使數據具有統計學意義，但考慮到我們只有 3 個數據點，0.12 的相對較小數值即使在這一點上不太顯著，也是很有希望的。

畢竟我們只有這些數據。因此，我們可以將衰減推斷到下一個峰值，該峰值與趨勢的偏差約爲 78%，基本上接近 2 倍。

我們可以回到 Desmos 應用程序，計算下一個周期頂點的趨勢值，這個頂點應該在 2025 年底。

順便提一下，以下是一個查找兩個日期之間天數的好方法：

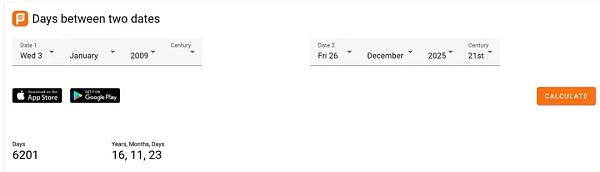
峰值的不確定性可能長達 2-3 個月，但這應該能爲我們提供一個粗略的估計值。

因此，從 2009 年 1 月 3 日（創世紀區塊）到預計的 4 個周期頂部之間大約有 6201 天。

讓我們將其輸入 Desmos 應用程序：

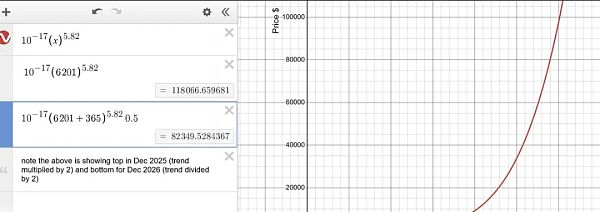
應用程序顯示趨勢值約爲 118,066 美元。

因此，估計的最高值是

頂部 = 118,000 + 78 / 100 * 118,000 = 210,000 美元。

因此，如果其他一切保持不變，這似乎是一個科學有效的估算周期頂部的方法。

我們還添加了對底部的估計，通常爲歷史趨勢的 50% 或略低於歷史趨勢。冪律理論對底部的預測比對頂部的預測要強得多。

趨勢值接近 165000 美元，底部應爲該值的一半左右。四舍五入到下一個整數，我們得出

下一個周期的底部 = 165,000 * 0.5 = 83,000 美元。

這些都是粗略的估計，但與我們的完整模型是一致的，該模型試圖包含一般的冪律趨勢、50-60%的硬底部、4 年周期的正弦波振蕩以及與上述計算結果類似的指數衰減。

見下圖：

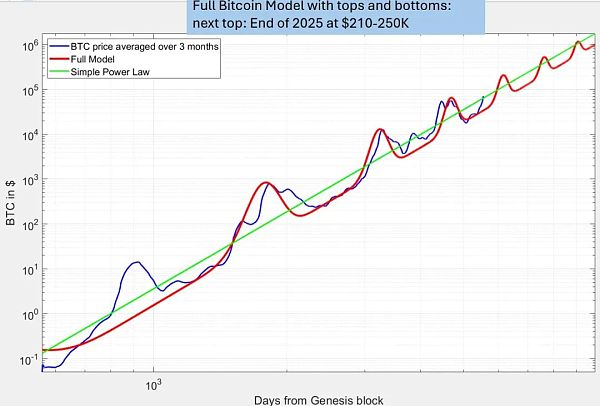
結論

當然，這些都是粗略的估計，但都是基於我們對比特幣的縮放特性及其非常可靠（迄今爲止）的周期性的理解。這些預測應該謹慎對待，但希望對比特幣投資者有用。

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。

標題：一種估算比特幣泡沫大小的科學方法

地址：https://www.torrentbusiness.com/article/103708.html

標籤：